You have a 2D vector: $$ \tag{1.1} v = (v_1, v_2) $$

You can calculate their length using: $$\tag{1.2} ||v|| = \sqrt{v_1^2 + v_2^2} $$

You achieve this by making the dot product of the vector by itself:$$\tag{1.3}||v||^2 = v \cdot v \Leftrightarrow ||v|| = \sqrt{v \cdot v}$$

But where pythagorean theorem applies? Let's rememeber the right triangle!

The image above, reminds you this formula: $$\tag{1.4} c^2 = a^2 + b^2 \Leftrightarrow c = \pm \sqrt{a^2 + b^2}$$

As you can see, we got a similar equation as $(1.2)$. This means the length of a 2D vector is the length of the hypotenuse of a right triangle.

Our 2D vector $v$ has the following components: $(4,3)$, Let's plot it in a cartesian plane:

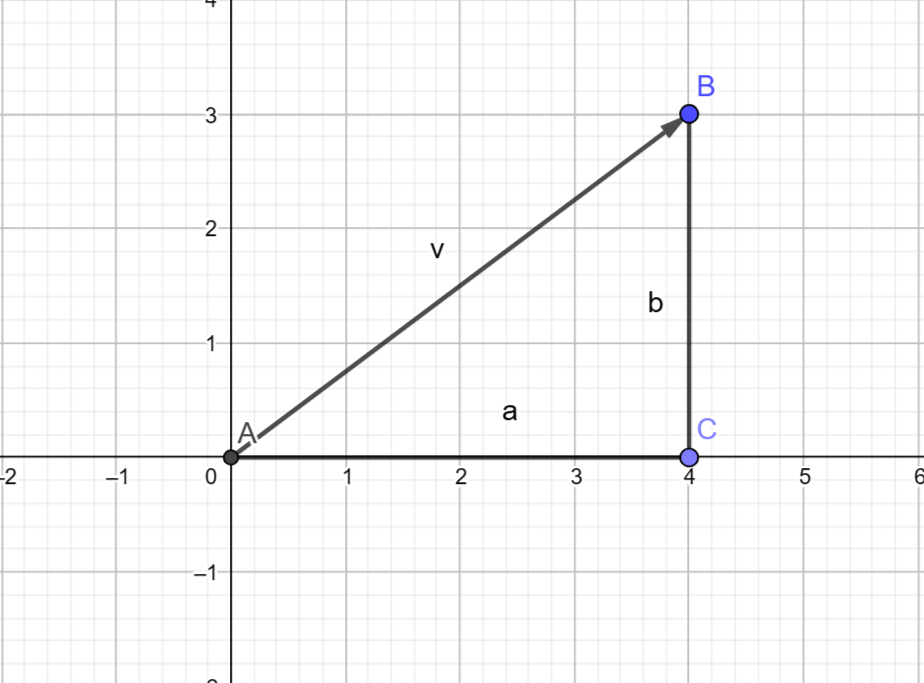
Vector $v$ creates a right triangle with its own coordinates. The segment $a = 4$ and segment $b = 3$, using the theorem we have: $$ \tag{1.5}v^2 = a^2 + b^2 \Leftrightarrow v^2 = 25 \Leftrightarrow v = \pm \sqrt{25}$$ So $v = 5$ which is not the best representation since $v$ is a vector (we keep it as vector in the triangle but it is a segment in that context). So it's more like: $||v|| = 5$.

It's cool right? Thinking about a vector length as a hypotenuse and not just a formula to memorize. Although it only works with 2D vectors, right? The answer is no, you can generalize it to any N-dimension vector! All you need is a little trick before calculating the square root.

Now imagine you have a vector $v = (1,2,4,5)$. How can you calculate its length using pythagorean theorem?

First of all, you need to decompose your vector $v$ in vectors with only 2 non-zero components. In this case we can have: $(1,2,0,0)$ and $(0,0,4,5)$.

Let's represent each vector in a plane, since the 0 components are on the origin.

The first vector could be in plane $xy$ with $a = 1$ and $b = 2$. So $c^2 = 1^2 + 2^2$.

The second vector could be in plane $zw$ with $a = 4$ and $b = 5$. So $c^2 = 4^2 + 5^2$.

Now, we've got the squared sides, to calculate each hypotenuse, we sum them up and take the square root: $$\tag{1.6} ||v|| = \sqrt{1^2 + 2^2 + 4^2 + 5^2} = \sqrt{46}$$

What we are doing here, is representing individual parts of the vector as a vector collinear to a plane, e.g 1 and 2 are the x and y coordinates of $v$, respectively, which will be collinear to $xy$ plane.

After calculating the squared sides of all individual parts, we sum them up like they're a big line that we're trying to calculate its length. Since we're using pythagorean theorem we need to put them sum as a radicand (number under square root symbol).

I recommend you read this algebraic proof about pythagorean theorem to understand why $c^2 = a^2 + b^2$ makes sense.

In the end it's simpler to use $||v|| = \sqrt{v_1^2 + v_2^2 + ... + v_n^2}$, but it's fun and give you another perspective on how to think about vector lengths.